「円の面積?半径×半径×3.14でしょ?」とすぐに答えてそれで済むのなら、あなたはこのブログを訪問しないでしょう。一言で「円の面積」と言っても、実は根が深く、奥が深いのです。
(ところで、算数のできる子には、「なんでそういう式になるの?」とか「3.14って何?」とか問い詰めてみましょう。)
学校での円の面積の教え方
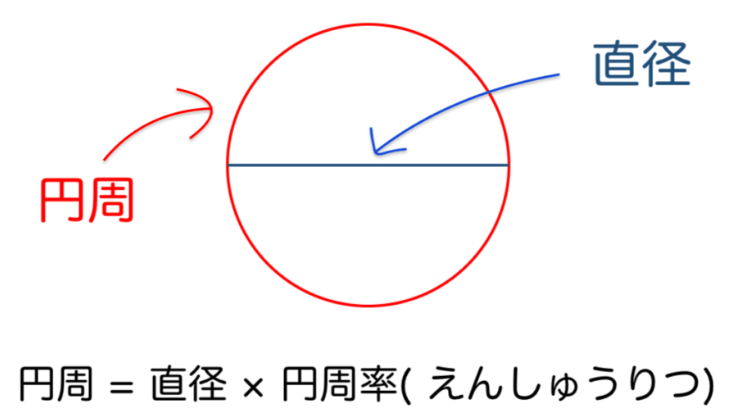
小学校の算数では、6年生で円の面積を扱うことになっています。ただし、5年生で円周が直径の約3.14倍であることを学習していることが前提となっています。
その上で、教科書や模型を使って下の図のようにして面積を求めることができることを理解します。

円の面積の教え方 第1の前提は円周を求められるか
すなわち、たて(半径)×横(円周の1/2)の長方形の面積に置き換えて理解するわけです。ここで、横とは円周の1/2に当たりますから、5年生で学習した円周=直径×3.14が分かっていないと式を立てられません。
面積という基本的概念が分かっていますか?
もし、ここまでの説明で理解できないとすれば、面積という概念そのものが身についてないことが考えられます。その場合は、4年生の算数にもどって教えなおす必要があります。
これ、非常に大事なことなので丁寧に教えましょう。中学生になっても面積と体積の概念や単位があやふやな子が結構多いのです。
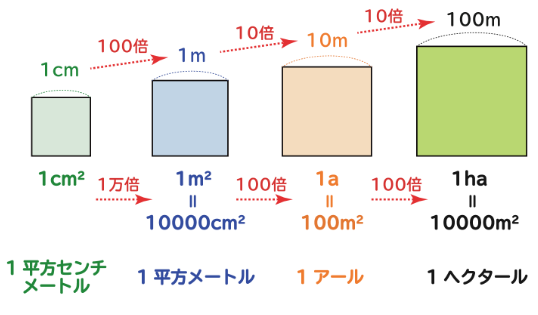
この図は、6年生で学習する単位関係ですが、扱う時間数が少ないので中学校に入っても苦労する子が多いので、できる限り機会を見て何度も教えたいものです。
この図の左端の「1辺が1cmの正方形の広さ」のことを「1平方センチメートル」と言い、「1㎠」と書く、と教えます。式にすると、1cm×1cm=1㎠。cmの右肩の小さな2は、cm×cmでcmを2回かけたという意味であることを教えます。
では、たてが2cm、横が3cmならば、2cm×3cm=6㎠、すなわち1㎠が6つ分です。これで、長方形の面積が理解できました。
小学生に円の面積を教える前にかけ算は大丈夫?
さて、面積の概念や求め方が分かっていても、小数のかけ算でつまずいていたのでは円の面積は求められません。
これも4年生での学習なので確認しておきましょう。